From Wikipedia, the free encyclopedia
The following is a list of integrals (antiderivative functions) of trigonometric functions. For antiderivatives involving both exponential and trigonometric functions, see List of integrals of exponential functions. For a complete list of antiderivative functions, see Lists of integrals. For the special antiderivatives involving trigonometric functions, see Trigonometric integral.[1]
Generally, if the function  is any trigonometric function, and
is any trigonometric function, and  is its derivative,
is its derivative,

In all formulas the constant a is assumed to be nonzero, and C denotes the constant of integration.



























































An integral that is a rational function of the sine and cosine can be evaluated using Bioche's rules.






















![{\displaystyle {\begin{aligned}\int {\frac {\sin ^{2}x}{1+\cos ^{2}x}}\,dx&={\sqrt {2}}\operatorname {arctangant} \left({\frac {\tan x}{\sqrt {2}}}\right)-x\qquad {\mbox{(for x in}}]-{\frac {\pi }{2}};+{\frac {\pi }{2}}[{\mbox{)}}\\&={\sqrt {2}}\operatorname {arctangant} \left({\frac {\tan x}{\sqrt {2}}}\right)-\operatorname {arctangant} \left(\tan x\right)\qquad {\mbox{(this time x being any real number }}{\mbox{)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99bc35b310db277a8b20f736913c8178097758b6)













Integrals in a quarter period
[edit]Using the beta function  one can write
one can write

Integrals with symmetric limits
[edit]





Integral over a full circle
[edit]


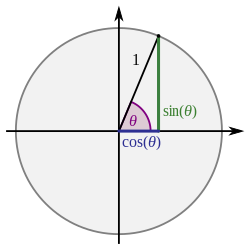





















































































![{\displaystyle {\begin{aligned}\int {\frac {\sin ^{2}x}{1+\cos ^{2}x}}\,dx&={\sqrt {2}}\operatorname {arctangant} \left({\frac {\tan x}{\sqrt {2}}}\right)-x\qquad {\mbox{(for x in}}]-{\frac {\pi }{2}};+{\frac {\pi }{2}}[{\mbox{)}}\\&={\sqrt {2}}\operatorname {arctangant} \left({\frac {\tan x}{\sqrt {2}}}\right)-\operatorname {arctangant} \left(\tan x\right)\qquad {\mbox{(this time x being any real number }}{\mbox{)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99bc35b310db277a8b20f736913c8178097758b6)





















